离散数学课程笔记

离散数学课程笔记

Chapter1 命题逻辑的基本概念

命题与连接词

否定、析取、合取、蕴含、等价连接词

命题公式及其赋值

  • 命题常项与命题变项
  • 合式公式：命题变元用联结词和圆括号按照一定逻辑关系连接起来的符号串 image-20230308193357562
  • 公式层次：单个命题算0层，运算一次加一层 image-20230308193421302
  • 赋值：对公式A中的全部命题变项全部指定一个值，称为对A的赋值/解释 成真赋值：使得公式A值为1的赋值，称为成真赋值。成假赋值同理
  • 真值表：公式A在所有赋值下的取值情况列成的表。
    • 求真值表时，首先将公式中n个命题变项按下标或字母序排列好
    • 纵向是2n个赋值，从0000开始，到1111结束
    • 横向按层次列出各子公式，求出不同赋值下的子公式值，并进而得出公式A的值
  • 重言式/永真式、矛盾式/永假式、可满足式

Chapter2 命题逻辑等值演算

等值式

  • 等值：命题公式A、B构成的等价式\(A\lrarr B\)为永真式，则称A与B等价，记作\(A\Leftrightarrow B\)。注意区别等价联接与公式等价的区别，即后者要求的是永真，在所有赋值下均为真。

  • 16个等值模式

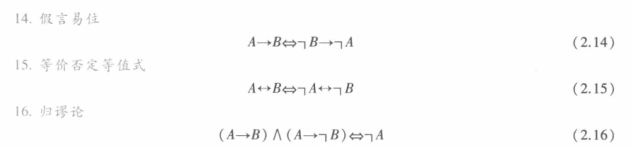
    image-20230308195413790 image-20230308195433705

析取范式与合取范式

  • 命题变项及其否定称为文字，仅由有限个文字构成的析取/合取式称为简单析取/合取式

  • 简单析取式是重言式，当且仅当其同时含有某个命题变项及其否定式

    简单合取式是重言式，当且仅当其同时含有某个命题的变项及其否定

  • 析取范式：有限个简单合取式，的析构，构成的命题公式 合取范式：有限个简单析取式，的合取，构成的命题公式

  • 析取范式是矛盾式，当且仅当每个简单合取式都是矛盾式

    合取范式是重言式式，当且仅当每个简单析取式都是重言式

  • 范式存在定理：任一公式命题，都存在与之等值的析取范式与合取范式

  • 求给定公式的范式步骤：

    1. 消去联结词\(\rarr\;、\lrarr\)
    2. 使用双重否定率消除双重否定符，用德摩根率内移否定符
    3. 使用分配律：求析取范式时，使用\(\land\)对\(\lor\)的分配率，求合取范式反之

  • 极小项：对有n个命题变项的简单合取式，对每个命题变相（或其否定式），均出现且仅出现一次，且按下标或字典序由小到大排列，则称其为一个 极小项。 极大项：把极小项的定义中，简单合取式换位简单析取式即可。

  • 极小项与极大项的性质：

    • 共有2n个极小项，且对每一个极小项，有且仅有一组成真赋值，根据成真赋值对应的十进制数，可以将其命名为mi
    • 共有2n个极大项，且对每一个极大项，有且仅有一组成假赋值，根据成真赋值对应的十进制数，可以将其命名为Mi
    • \(\neg m_i \Leftrightarrow M_i\ ,\ \neg M_i \Leftrightarrow m_i\)

  • 主析取范式：所有简单合取式都是最小项的析取范式，称为主析取范式 主合取范式：所有简单析取式都是最大项的合取范式，称为主合取范式

  • 任何命题公式，都存在唯一一个与之等值的主析取范式，与主合取范式 证明：

  • 求主析取范式的步骤：如上述存在性证明中所示，若某一简单合取式中，不含有命题变元\(p_j\)，则对其合取上\((p_i \lor\neg p_i)\)，（同一律+排中律），重复这一过程，直至每一个简单合取式都包含全部的n个命题变元，然后将其排列为最小项形式，并用对应的mi代替 求主合取范式的步骤：思想同上，区别在去，对每一个不合格的简单析取式，（同一律与矛盾律）都析取上一个\((p_i\land \neg p_i)\)

  • 主析取范式的用途：

    • 求公式的成真赋值与成假赋值： 若公式A的主析取范式中，有 s 个最小项，则A有 s 个成真赋值，对应极小项的下标。剩余 2n - s 个成假赋值。（析取范式，有一个极小项为真就行）
    • 判断公式类型：
      • 公式A为重言式，当且仅当A的主析取范式含有全部 2n 个极小项
      • 公式A为矛盾式，当且仅当A的主析取范式含有 0 个极小项
      • 公式A为可满足式，当且仅当A的主析取范式至少含有一个极小项
    • 判断两个命题公式是否等值： 假设命题公式A与B共含有 n 个命题变元，按 n 个命题变元求出其对应的主析取范式 \(A^`、B^`\)，若 \(A^`\Lrarr B^`\)，则\(A \Lrarr B\)，否则 \(A \nLeftrightarrow B\)

  • 由主析取范式求主合取范式：找出所有未出现在主析取范式中的极小项，其下标对应的极大项合取，即为主合取范式。证明：

  • n 个命题变项的主析取/合取范式，共有 \(2^{2^n}\) 个。（因为有 2n 个最小项，组合数求和）

  • \(A\Lrarr B\)，当且仅当二者有相同的真值表，也当且仅当二者有相同的范式。因此，范式与真值表，就是描述命题的两种不同的、等价的标准形式，二者相互确定。

  • 至此，判断两命题公式等价的方法有：真值表法、等值演算法、范式法

联结词的完备集

  • n 元真值函数 \(F:\{0,1\}^n\rarr \{0,1\}\)，其中定义域 {0,1}n={00...0, 00...1, ..., 11...1}，值域={0,1}

  • n 个命题变元可以构成 \(2^{2^n}\) 个真值函数，即一元真值函数有 4 个，二元真值函数有 16 个

  • 每个真值函数都可表示成唯一的一个主范式，每个主范式对应无穷个命题公式，每个命题公式有唯一的真值函数

  • 如果 n 元真值函数，可以仅由集合S中含有的联结词构成的公式表示，则称S是一个联结词的完备集

  • \(\{\neg,\ \land,\ \lor\}\) 是联结词完备集

  • 与非联结词 \(\uparrow\) ，有 \(p\uparrow q \Lrarr \neg(p \land q)\)

    或非联结词 \(\downarrow\) ，有 \(p\downarrow q \Lrarr \neg(p \lor q)\)

  • \(\{\uparrow,\ \downarrow\}\) 是一个联结词完备集

Chapter3 命题逻辑的推理理论

推理的形式结构

  • 设 \(A_1,A_2,...,A_k\) 和 B 都是命题公式，若对于 \(A_1,A_2,...,A_k\) 和 B 中出现的所有命题变项的任意一组赋值，要么 \(A_1,A_2,...,A_k\) 为假；要么为真，且 B 也为真。那么此时就称，从前提 \(A_1,A_2,...,A_k\) 推出结论 B 的推理是有效的/正确的，并称B为有效的结论。（==注意，说的推理是正确的，并没有说结论是正确的==）有几点说明：

    1. 前提推出结论的正确与否，与诸前提的排列次序无关。
    2. 前提是一个有限的公式集合，记为 \(\varGamma\)，由前提 \(\varGamma\) 推出结论 B 的推理记为 \(\varGamma \vdash B\)，或\(\{A_1,A_2,...,A_k\}\vdash B\)，叫做推理的形式结构。如果推理是正确的，则记为 \(\varGamma \vDash B\)，否则记为 \(\varGamma \nvDash B\)
    3. （类似蕴含），前提与结论共有四种可能取值情况，只要不是前提为真时结论为假，都称推理是正确的。
    4. 此处的推理只是形式推理，推理正确并不能保证结论正确，因为前提可能不成立。前提为假的时候，我们也成推理是正确的。但是通常我们认为，只有正确的前提，才能推出正确的结论。

  • 由命题公式 \(A_1,A_2,...,A_k\) 推出 B 的推理是正确的，当且仅当 \(A_1\land A_2\land ...\land A_k\rarr B\) 是重言式

  • 推理的形式结构 \(\{A_1,A_2,...,A_k\}\vdash B\) 等同于蕴含式 \(A_1,A_2,...,A_k\rarr B\) 推理正确 \(\{A_1,A_2,...,A_k\}\vDash B\) 等同于 \(A_1\land A_2\land ...\land A_k\Rightarrow B\)，其中\(\Rightarrow\)表示蕴含式为重言式

  • 判断蕴含式是否为重言式的方法：真值表法、等值演算法、主析取范式法

自然推理系统 \(P\)

  • 定义一个形式系统 \(I\) 由四部分组成

    1. 非空的字母表 \(A(I)\)
    2. \(A(I)\) 中符号构成的合式公式集 \(E(I)\)
    3. \(E(I)\) 中一些特殊的公式组成的公理集 \(A_X(I)\)
    4. 推理规则集 \(R(I)\)

    将\(I\) 记为四元组 \(<A(I),E(I),A_X(I),R(I)>\)，其中 \(<A(I),E(I)>\) 是 \(I\) 的形式语言系统， \(A_X(I),R(I)>\) 是\(I\) 的形式演算系统。形式系统分为自然推理系统与公里推理系统

  • 自然推理系统：从任意给定的前提出发，运用系统中的推理规则进行演算，得到的命题即为推理的结论。结论是有效的，但是不一定为重言式 公理推理系统：只能从若干条给定的公里出发，运用系统中的推理规则进行推理，得到的有效结论一定是重言式，称为系统中的公理。

  • 自然推理系统的定义如下： image-20230309132305844

  • 证明的概念：

  • 证明法：

    1. 附加前提证明法：把结论的前提，纳入到证明的前提中去，只需证明结论的结论有效性即可
    2. 归谬法：将欲证明结论的否定作为前提，利用现有的条件推出矛盾式来，即可证明原结论的有效性。
    3. 反证法、穷举法、存在性与唯一性证明……

Chapter4 一阶逻辑的基本概念

​ 命题逻辑具有局限性，因为它不能很好的描述个体与整体之间的内在联系与数量关系，因此引入量词的概念。这就是一阶逻辑所研究的内容。一阶逻辑又称一阶谓词逻辑或谓词逻辑。

一阶逻辑命题符号化

个体词、谓词、量词是一阶逻辑命题符号化的三个基本要素

  • 个体词：研究对象中可以独立存在的具体或抽象的客体。具体指代的叫个体常项，抽象泛指的叫个体变项。个体变项的取值范围称为个体域/论域，他可以是有限集，也可以是无限集。表示宇宙间一切事物的叫全总个体域。
  • 谓词：用来刻画个体词性质，及个体间关系的词，常用字母 \(F、G、H\) 表示。同样的，表示具体关系的叫谓词常项，表示抽线关系的叫谓词变项，他们都用大写字母表示。有时为了做出一些区分，还需要引入特性谓词
  • 量词：全称量词 \(\forall\)，存在量词 \(\exists,\nexists\)
  • 例子： image-20230309170304875
  • 对于含有 n 元谓词的命题要注意：
    1. 命题中的性质谓词符号化为一元谓词，而表示关系的符号华为多元谓词
    2. 根据实际意义选择全称或存在量词
    3. 一般来说，多个量词出现时，他们的顺序不能互换
    4. 命题的符号化形式不唯一

一阶逻辑公式及解释

course
#math
离散数学课程笔记
https://captainwc.github.io/2023/03/20/离散数学课程笔记/
作者
kk
发布于
2023年3月20日
许可协议